Turunan dasar
Aturan - aturan dalam turunan fungsi adalah :
f(x), maka f'(x) = 0
Jika f(x) = x, maka f’(x) = 1
Aturan pangkat : Jika f(x) = xn, maka f’(x) = n X n – 1
Aturan kelipatan konstanta : (kf) (x) = k. f’(x)
Aturan rantai : ( f o g ) (x) = f’ (g (x)). g’(x))
Turunan jumlah, selisih, hasil kali, dan hasil bagi dua fungsi
Misalkan fungsi f dan g terdiferensialkan pada selang I, maka fungsi f + g, f – g, fg, f/g, ( g (x) ≠ 0 pada I ) terdiferensialkan pada I dengan aturan :
( f + g )’ (x) = f’ (x) + g’ (x)
( f – g )’ (x) = f’ (x) + g’ (x)
(fg)’ (x) = f (x) g’(x) + g’(x) f(x)
((f)/g )’ (x) = (g(x) f' (x)- f(x) g' (x))/((g(x)2)
Turunan fungsi trigonometri:
d/dx ( sin x ) = cos x[5]
d/dx ( cos x ) = - sin x[5]
d/dx ( tan x ) = - sec2 x[5]
d/dx ( cot x ) = - csc2 x[5]
d/dx ( sec x ) = sec x tan x[5]
d/dx ( csc x ) = -csc x cot x[5]
Turunan fungsi invers
(f-1)(y) = 1/(f' (x)), atau dy/dx = 1/(dx/dy)
Berikut ini adalah 3 gambar grafik trigonometri yang mendasar, yaitu grafik fungsi sinus, grafik fungsi kosinus dan grafik fungsi tangen. Untuk grafik fungsi trigonometri yang lainnya, bisa digambar di software grafik yang pembaca miliki.
Cosinus
Gambar grafik kosinus ini, ketika 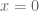 , maka nilai
, maka nilai 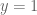 . Menggambar grafik trigonometri sinus dan kosinus ini sangat mudah untuk diingat. Ingat saja lengkungannya dan periodiknya. Grafik kosinus dimulai dari 1, kemudian ketika
. Menggambar grafik trigonometri sinus dan kosinus ini sangat mudah untuk diingat. Ingat saja lengkungannya dan periodiknya. Grafik kosinus dimulai dari 1, kemudian ketika 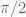 , grafiknya memotong sumbu x. ketika
, grafiknya memotong sumbu x. ketika 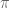 , grafiknya bernilai
, grafiknya bernilai 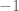 , dan seterusnya sampai
, dan seterusnya sampai  .
.
Grafiknya dicerminkan terhadap sumbu y. perhatikan gambar! Ingat. suatu fungsi yang gambar grafiknya dicerminkan terhadapa sumbu y, maka fungsi itu adalah fungsi genap. Jadi, nilai  . Sehingga kita bisa mudah mengingat kenapa cos(-150) itu sama dengan cos(150).
. Sehingga kita bisa mudah mengingat kenapa cos(-150) itu sama dengan cos(150).
Penggambaran grafik ini sangat membantu untuk mempermudah menentukan nilai trigonometrinya. Kita sudah tidak perlu menghafal kuadran-kuadran, nilai positif dan negatif.
Dengan melihat grafik dari fungsinya saja kita dengan mudah bisa menentukan nilai trigonometrinya.
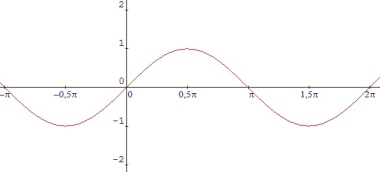
Sinus
Gambar grafik sinus dimulai dari 0. Kemudian ketika nilai x sama dengan 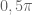 , maka grafik tersebut mencapai ketinggian 1. Dan ketika nilai x sama dengan
, maka grafik tersebut mencapai ketinggian 1. Dan ketika nilai x sama dengan 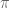 , maka grafiknya bernialai 0. Bisa dilihat pada gambar tersebut.
, maka grafiknya bernialai 0. Bisa dilihat pada gambar tersebut.
Fungsi sinus adalah fungsi ganjil. Perhatikan saja grafiknya. Gambar grafiknya dicerminkan terhadap titik 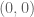 . Ingat definisi fungsi ganjil, yaitu
. Ingat definisi fungsi ganjil, yaitu  . Sinus adalah fungsi ganjil. Ini bisa dimanfaatkan untuk menentukan nilai dari sin(-60). Misalnya. Sin(-60) sama dengan –sin(60).
. Sinus adalah fungsi ganjil. Ini bisa dimanfaatkan untuk menentukan nilai dari sin(-60). Misalnya. Sin(-60) sama dengan –sin(60).
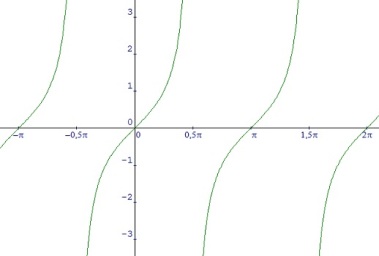
Tangen
Gambar grafik dari tangent cukup aneh bagi kita yang baru pertama melihatnya. Perlu diingat bahwa tangent itu sama dengan sinus per cosines. Jadi, titik-titik pada grafik tangent itu sama dengan titik-titik pada grafik sinus dibagi dengan titik-titik pada grafik cosines. Perhatikan saja untuk 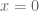 , titik pada saat
, titik pada saat 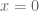 pada grafik sinus adalah 0, dan padagrafik cosines adalah 1. Sehingga, pada grafik tangent akan sama dengan
pada grafik sinus adalah 0, dan padagrafik cosines adalah 1. Sehingga, pada grafik tangent akan sama dengan 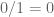
Inilah yang bisa kalian pahami, mengapa tangent 90 itu tidak didefinisikan.
Tentunya karena pembagian dengan nol.
Periodik dari ketiga fungsi trigonometri
Periodik adalah perulangan. Definisi periodic adalah 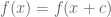 , maka fungsi itu dikatakan periodic dengan periode c.
, maka fungsi itu dikatakan periodic dengan periode c.
Fungsi sinus, cosines dan tangent adalah fungsi yang periodic. Karena ada c, sehingga 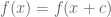 . Yaitu ketika c itu sama dengan
. Yaitu ketika c itu sama dengan  . Perhatikan saja bahwa nilai dari
. Perhatikan saja bahwa nilai dari 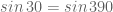
Sinus dan Cosinus
Fungsi sinus dan fungsi cosines adalah fungsi yang periodik dengan periode  . Ini sangat membantu untuk menentukan suatu nilai trigonometri yang sangat besar. Misalnya, berapakah nilai dari
. Ini sangat membantu untuk menentukan suatu nilai trigonometri yang sangat besar. Misalnya, berapakah nilai dari 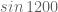 . Maka kita tentunya bisa memanfaatkan peridik dari fungsi tersebut.
. Maka kita tentunya bisa memanfaatkan peridik dari fungsi tersebut.
Tangen
Berbeda dengan sinus dan kosinus. Fungsi tangent juga merupakan fungsi yang periodic, tetapi besar periodenya berbeda dengan fungsi sinus dan fungsi cosines. Periode dari tangent adalah 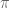


Tidak ada komentar:
Posting Komentar